06-logistic回归
数据集
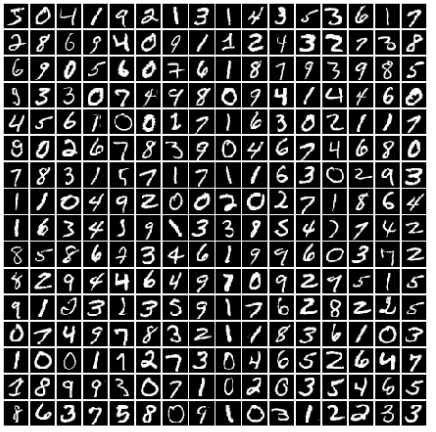

激活函数
logistic回归模型
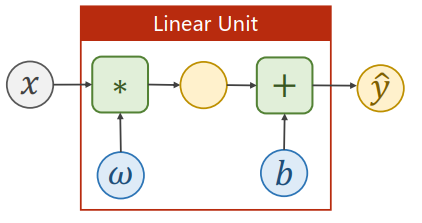
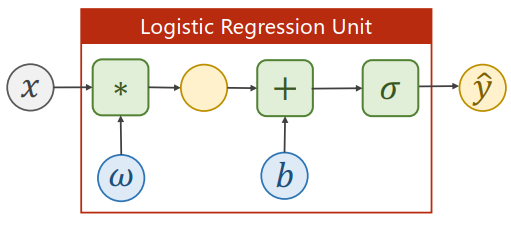
损失函数
对比
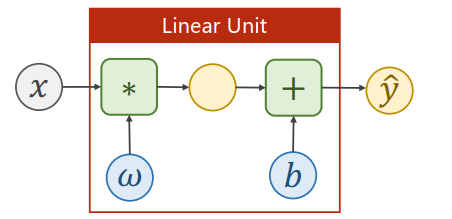
实现
最后更新于
这有帮助吗?






最后更新于
这有帮助吗?
这有帮助吗?
import torchvision
# torchvision 是一个数据集集合的模块
## root设置数据集存放的路径,train表示是否下载训练集,download表示是否进行下载
train_set = torchvision.datasets.MNIST(root="./数据集/mnist",
train=True,download=True)
test_set = torchvision.datasets.MNIST(root="./数据集/mnist",
train=False,download=True)import torchvision
# torchvision 是一个数据集集合的模块
## root设置数据集存放的路径,train表示是否下载训练集,download表示是否进行下载
train_set = torchvision.datasets.CIFAR10(root="./数据集/cifar10",
train=True,download=True)
test_set = torchvision.datasets.CIFAR10(root="./数据集/cifar10",
train=False,download=True)import torch
class LinearModel(torch.nn.Module):
def __init__(self,):
super(LinearModel,self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self,X):
y_pred = self.linear(x)
return y_predclass LogisticRegressionModel(torch.nn.Module):
def __init__(self,):
super(LogisitcRegressionModel,self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self,X):
# 调用sigmoid激活函数
y_pred = torch.sigmoid(self.linear(X))
return y_predx_data = torch.Tensor([
[1.0],[2.0],[3.0]
])
y_data = torch.Tensor([
[0],[0],[1]
])
class LogisticRegressionModel(torch.nn.Module):
def __init__(self,):
super(LogisticRegressionModel,self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self,X):
y_pred = torch.sigmoid(self.linear(X))
return y_pred
def fit(self,X,y):
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(self.parameters(),lr=0.01)
for epoch in range(1000):
y_pred = self.forward(x_data)
loss = criterion(y_pred,y)
print(epoch,loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
model = LogisticRegressionModel()
model.fit(x_data,y_data)import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,10,200)
x_t = torch.Tensor(x).view((200,1))
y_t = model(x_t)
y = y_t.data.numpy()
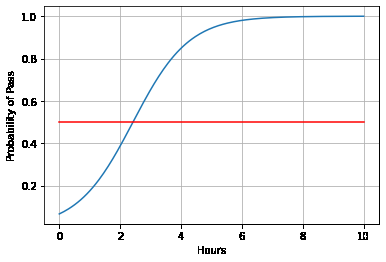
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel("Hours")
plt.ylabel("Probability of Pass")
plt.grid()
plt.show()