谱聚类
基本概念
定义无向图$G={V,E,W}$,其中,$V$为图的顶点,$E$为图的边,$W$为图中边的权值矩阵。
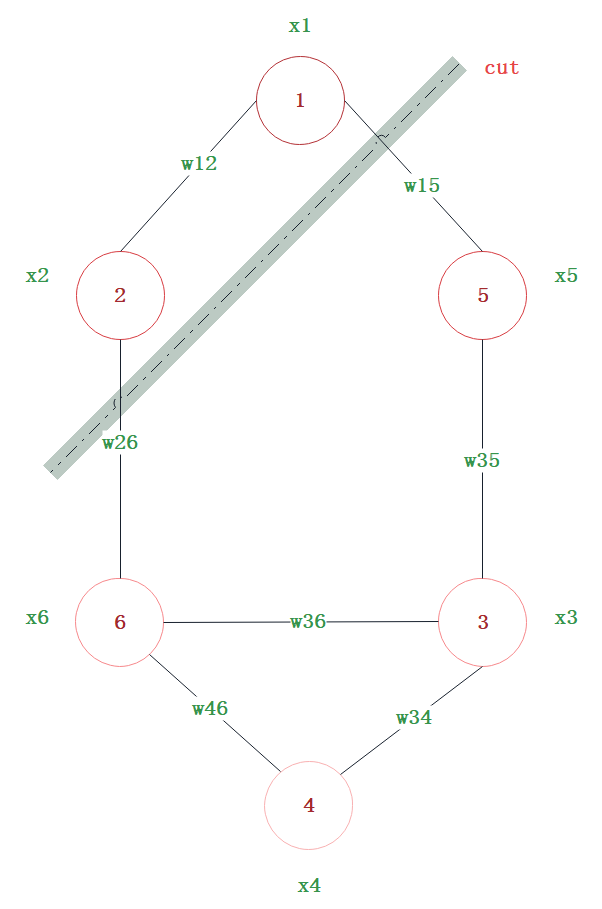
定义顶点的度为该顶点与其他顶点连接权值之和:
度矩阵$D$为:
图的邻接矩阵(相似矩阵)$W$:
对于$V$的一个子集$A\subset V$:
相似矩阵
邻接矩阵$W$:由任意两点之间的权重值$w_{ij}$组成的矩阵。通常手动输入权重,但是在谱聚类中,只有数据点的定义,并没有直接给出这个邻接矩阵,那么如何构造邻接矩阵?
基本思想:距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,不过这仅仅是定性,需要定量的权重值。一般来说,我们可以通过样本点距离度量的相似矩阵$S$来获得邻接矩阵$W$。
构造方法:这里采用全连接法进行构造邻接矩阵。可以采用不同的核函数来定义边权重,这里采用高斯核函数RBF:
拉普拉斯矩阵
拉普拉斯矩阵定义:
其中,$D$为度矩阵,$W$为邻接矩阵。
拉普拉斯矩阵的性质:
拉普拉斯矩阵是对称矩阵,其所有特征值都是实数
对于任意向量$f$,有:
于是,可以得知:
拉普拉斯矩阵是半正定的,且对应的n个实数特征值都大于等于0$(0=\lambda_1\leq \lambda_2 \leq \cdots \leq \lambda_N)$,且最小的特征值为0,对应的特征向量是单位向量。
由图分割问题到谱聚类问题
对于无向图$G$的切割图,目标是将图$G$切分成相互没有连接的$k$个子图,每个子图点的集合为:
对于任意两个子图点的集合$A,B \subset V,A\cap B = \oslash$,定义$A$和$B$之间的切图之间的权重为:
对于k个子图点的集合,定义切图$cut$为:
其中,$\bar{A_i}$为$A_i$的补集(除去$A_i$子集以外其他的属于$V$的结点的集合)。
为了让切图可以让子图内的点权重和高(内部连接强),子图间的点权重和低(外部连接弱),需要使$cut$达到最小化。
优化目标:
为了避免最小切图导致的切图效果不佳,需要对每个子图的规模做出限定。这里得到了一个新的优化目标:
由上可知,算法的目标函数为:
由于求解的时候,不方便计算,于是设法将目标函数转换为矩阵的形式表达。
引入指示向量
令
其中,$y_i$是一个$k$维的向量,每一个维度的值为0或者1;$y_{ij}$表示第$i$个样本属于第$j$个类别,并且每个样本只能属于一个类别。
由上,可知目标函数为:
又,
现在已知$W$,$Y$,求$O$,$P$,注意$Y$矩阵是$N\times K$维的,行代表结点标号,列代表属于的类别,其中$y_{ij}$表示第$i$个样本属于第$j$个类别。
有,
于是,
其中,$N_K$表示在$N$个样本中,属于类别$k$的样本个数,且$\sum\limits_{k=1}^KN_k = N$,$N_k = |A_k|=\sum\limits_{i\in A_k} 1_N$,$1_N$表示元素全为$1$的$N\times 1$维向量。
有,
使用拉普拉斯矩阵的性质,简化$O$矩阵,如下:
由于,
令,
由$trace$性质可知,
其中,$O^{'}$与$O$的对角元素一样。
于是,有
定义$H$为新的指示向量:
有,
于是,
记,$H=D^{-\frac{1}{2}}F$,有$F^TF=I$,
注意$Y^TY$与$H^TH$表示的含义,两者的主对角线的值是相反的。
谱聚类实现
实现步骤


导入包
谱聚类
生成数据
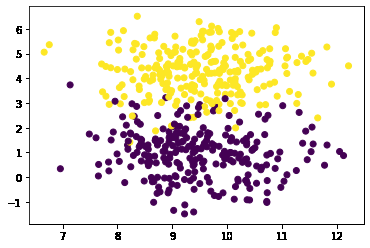
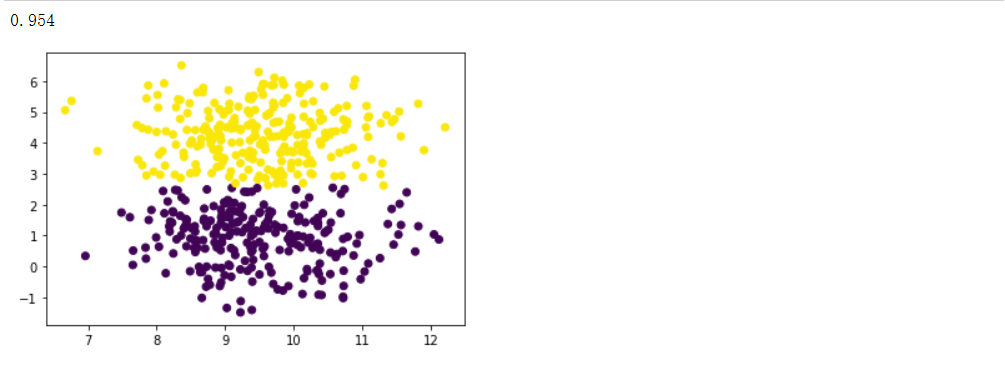
运行
最后更新于
这有帮助吗?
