05-用pytorch实现线性回归
回归
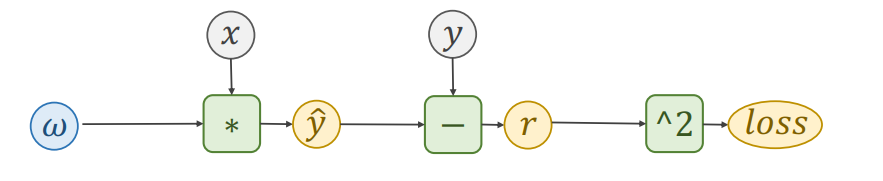
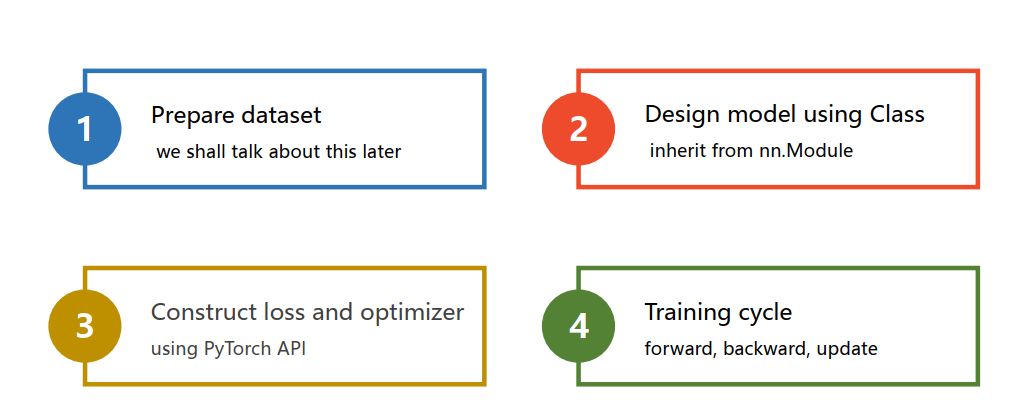
数据

设计模型
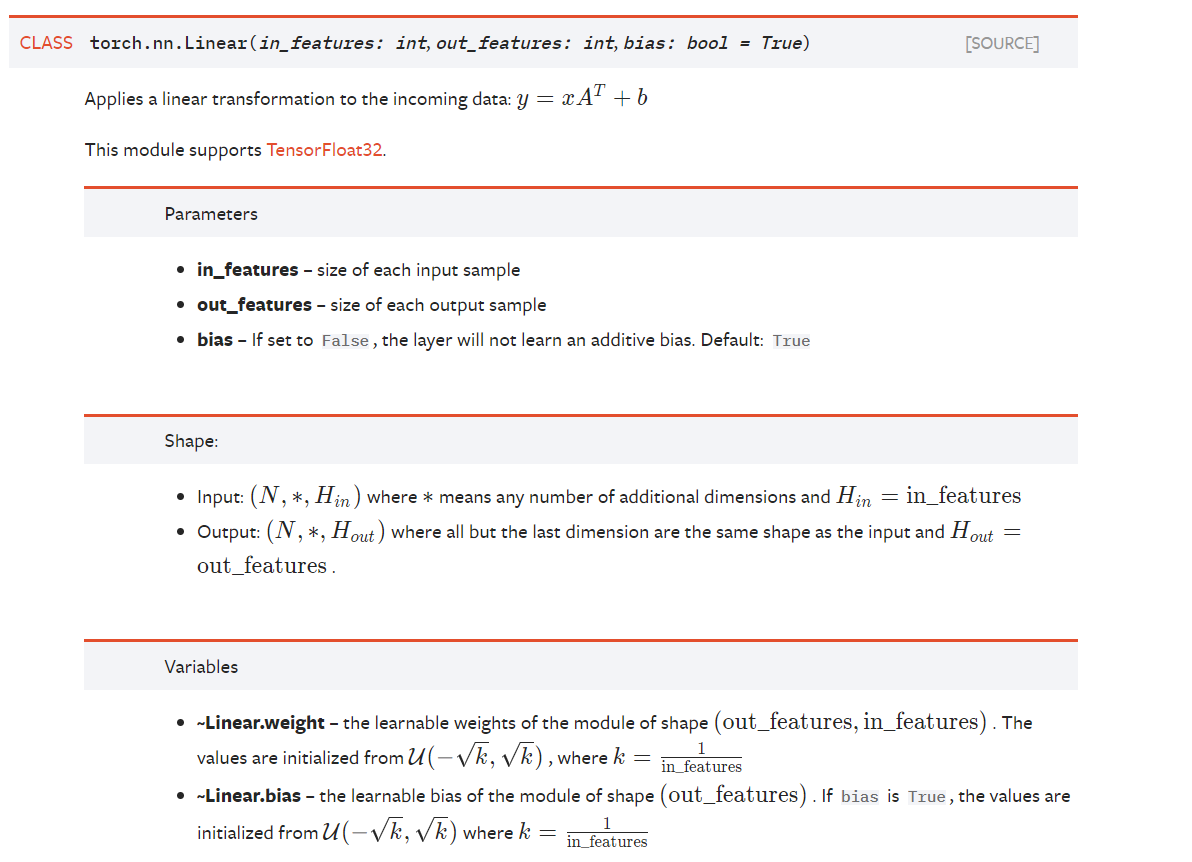
损失函数和优化器


前馈与反馈

最后更新于
这有帮助吗?







最后更新于
这有帮助吗?
这有帮助吗?
import torch
import numpy as np
data = np.array([
[1.0,2.0],
[2.0,4.0],
[3.0,6.0]
])
data = torch.Tensor(data)
x_data,y_data = data[:,:-1],data[:,-1]
x_data,y_dataclass LinearModel(torch.nn.Module):
def __init__(self,):
super(LinearModel,self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self,x):
y_pred = self.linear(x)
return y_pred
lm = LinearModel()class LinearModel(torch.nn.Module):
...class LinearModel(torch.nn.Module):
def __init__(self,):
super(LinearModel,self).__init__()
...
def forward(self,x):
...self.linear = torch.nn.Linear(1,1) def forward(self,x):
y_pred = self.linear(x) # 里面做了wx+b的运算
return y_predcriterion = torch.nn.MSELoss(reduction='sum') # 损失函数
optimizer = torch.optim.SGD(lm.parameters(),lr=0.01) # 优化器torch.optim.Adagrad
torch.optim.Adam
torch.optim.Adamax
torch.optim.ASGD
torch.optim.RMSprop
* torch.optim.Rprop
torch.optim.SGDfor epoch in range(100):
y_pred = lm(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()print("w=",lm.linear.weight.item())
print("b=",lm.linear.bias.item())x_test = torch.Tensor([[4.0]])
y_test = lm(x_test)
print("y_pred=",y_test.data)